La régularité du tempérament est un signe de perfection, à l’image d’une règle millimétrée n’étant pas là pour modifier les choses qu’elle mesure. Ce qui est intéressant avec cet outil, se voit dans son utilité permettant d’obtenir les informations recherchées. ___________________________________
L’histoire d’une rencontre avec le chiffre six
Ceci remonte avant le samedi 16 janvier 2021, 14:45:23. Cette date précise le moment de la création d’une image de référence, c’est celle qui est à gauche du titre principal. Tout cela a commencé parce que je suis curieux, et que j’aime chercher pour trouver, tout en ayant le plaisir et la chance de voir différentes expressions familières. L’automatisme de la programmation a diverses méthodes, comme l’itération par exemple. L’étude des nombres et de la division en particulier, à force de chercher, je suis tombé sur le nombre six comme diviseur. Il se passe quelque chose en divisant les nombres par six, leurs parties décimales présentent des signes de similitudes…
Le tissage des nombres décimaux peut-être envisagé en appliquant la division sur d’autres nombres entiers, car chacun d’eux, produit une nouvelle famille de nombres décimaux. Le nombre six, produit six nombres décimaux qui se répètent. Ça je le sais. Mais j’ignore tout des productions des autres nombres, qu’ils soient entiers ou bien décimaux. Cette étude est à la portée de tous ceux qui ont un calculateur, et beaucoup d’intéressement avec cette affaire.
Une simple définition des nombres.
Quand on divise les nombres par six, et on se trouve face à une répétition décimale. Devant une série de décimales, dont seules les parties entières changent. Faisant une série ayant un pas de six à chaque itération, mettant en rôle :
- Le chiffre six = Le diviseur commun.
- Les nombres entiers de 1 à 30.
- Les quotients des divisions.
- Les restes des divisions.
Le plus surprenant, c’est cette particularité de classifier les nombres. Mais, uniquement parce qu’ils sont ainsi. Les personnes qui ont créé les nombres ont découvert une source logique infinie. Ils ont su réaliser, avec homogénéité, la définition parlée, écrite et maintenant numérique.
Pour nous, les nombres sont partout, ces nombres qui parviennent à suivre les contours naturels de la vie. Ils ne sont certes pas parfaits, d’une part parce que la perfection est définie par la nature, et d’autre part, leurs perfections existent seulement, car on les utilise. Si tel le souhait était le développement des définitions convenables aux nombres, il serait fortement probable qu’un nombre infini d’explications sensationnelles rende un verdict sans fin. Ce jeu analytique conviendrait parfaitement à notre humanité, qui sans cesse évolue dans son savoir.
La constance des nombres :
Savez-vous que le chiffre un (1) a un point commun avec le chiffre (7) ?
Afin que vous compreniez que cette synchronisation, réalisée via le chiffre six (6), n’est pas factice, mais factuelle.
Factice :
Tant que l’explication n’est pas donnée au sujet de cette ordonnance, même si un tel alignement numérique n’est sûrement pas un effet de hasard. Ce fantastique ordre numérique a une réalité parfaitement appliquée, il est l’ombre d’une logique infinie.
Factuel :
Si seulement, le rangement était simplement fantastique. L’ordre est indiscutablement parfait, il est composé de nombres maniérés obéissants à des règles typiques. Les nombres se conjuguent aux temps définis comme ci :
- Les nombres pairs ou impairs.
Les magnifiques manipulations numériques.
Visiblement, les nombres ne présentent pas une grande difficulté intellectuelle. Ce n’est pas en les regardant qu’on pourrait deviner des qualités allant au-delà de leur parité…
Les nombres paritaires ou leurs activités ?
À l’origine, les nombres ont été créés par des maîtres comptables. Les opérations mathématiques forment l’invention du nombre, il n’empêche que le nombre est prioritaire dans l’expression générale du comptage. On peut parler de conjugaison mathématique lorsque le signe opérateur en soi le mode, et élémentairement, il y a quatre modes couramment utilisés (+ – * /).

Visite de la salle des machines mathématiques
Chaque opérateur amène ses descriptives, la plus basique des opérations inclut deux nombres opérationnels et un terme comme résultat. La multiplication est productive, la division définit un quotient, l’addition fournit une somme, la soustraction soumet une différence. Ainsi, quand on dira qu’untel nombre est multiple de trois, cela signifiera que le chiffre trois fait partie d’un des deux multiplicateurs.
À quoi bon refaire une éducation mathématique, quand il s’agit d’individus ayant un âge mûr. La mathématique est élémentaire, quel que soit le niveau de complexité, puisque la simplicité apparait en même temps que la consciente résolution.
Le centre algorithmique du calculateur informatique.
C’est une situation mathématique qui s’explique par la mathématique, le code source Python qui suit, est une ressource qui nous en dit suffisamment pour assimiler les catégories des nombres.
Partie du code d’analyse du type du nombre
dico = {1:[], 2:[], 3:[], 4:[], 5:[], 0:[]}
li = liste(range(1, 31))
for i in li:
reste = i % 6
dico[reste].append(i)
for kid, vi in dico.items():
print("\t", vi, "________")
for x in vi:
y = x / vi[0]
print("Kid: {} X {} Y: {}".format(kid, x, y))
Les lignes de codage alimentent le dictionnaire (dico) des restes de la division des nombres inclus dans la liste (li), afin de vérifier la concordance des nombres de la liste avec les restes comme diviseurs. D’un premier abord, on pourrait croire que les restes sont étrangers à la notion des multiples. Mais une fois que la vérification est terminée, on se trouve devant une réalité augmentée, étant la preuve d’une certaine concordance.
Partie du résultat du code d’analyse du type du nombre
[1, 7, 13, 19, 25] ________
Ki: 1 X 1 Y: 1.0
Ki: 1 X 7 Y: 7.0
Ki: 1 X 13 Y: 13.0 Multiples d’un (1)
Ki: 1 X 19 Y: 19.0 Nombres premiers ?!
Ki: 1 X 25 Y: 25.0
[2, 8, 14, 20, 26] ________
Ki: 2 X 2 Y: 1.0
Ki: 2 X 8 Y: 4.0
Ki: 2 X 14 Y: 7.0 Multiples de deux (2)
Ki: 2 X 20 Y: 10.0
Ki: 2 X 26 Y: 13.0
[3, 9, 15, 21, 27] ________
Ki: 3 X 3 Y: 1.0
Ki: 3 X 9 Y: 3.0
Ki: 3 X 15 Y: 5.0 Multiples de trois (3)
Ki: 3 X 21 Y: 7.0 Impairs
Ki: 3 X 27 Y: 9.0
[4, 10, 16, 22, 28] ________
Ki: 4 X 4 Y: 1.0
Ki: 4 X 10 Y: 2.5 Multiples de deux (2)
Ki: 4 X 16 Y: 4.0 Multiples de quatre (4)
Ki: 4 X 22 Y: 5.5 Une fois sur deux.
Ki: 4 X 28 Y: 7.0
[5, 11, 17, 23, 29] ________
Ki: 5 X 5 Y: 1.0
Ki: 5 X 11 Y: 2.2
Ki: 5 X 17 Y: 3.4 Nombres premiers ?!
Ki: 5 X 23 Y: 4.6
Ki: 5 X 29 Y: 5.8
[6, 12, 18, 24, 30] ________
Ki: 0 X 6 Y: 1.0
Ki: 0 X 12 Y: 2.0 Multiples de trois (3)
Ki: 0 X 18 Y: 3.0 Multiples de six (6)
Ki: 0 X 24 Y: 4.0 Pairs
Ki: 0 X 30 Y: 5.0
Même si la liste ne contient pas une infinité de nombres, les résultats resteront fiables et déterminants par rapport aux nombres premiers.
Les nombres premiers sont toujours alignés sur les rangs des restes un (1) et cinq (5).
Les tempéraments et les rayons sont en harmonie.
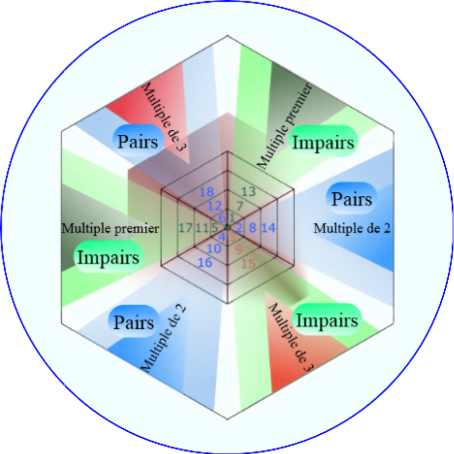
Comment ne pas remarquer, que cet alignement distinctif, est propre aux nombres.