Le sens du terme diatonique est revu à la baisse, dans sa définition.
Les tétracordes
La théorie des cordes
Définition du dictionnaire
La théorie est basée sur des objets assimilables à des cordes vibrantes…
Dictionnaire sur l’internet
En faisant en sorte qu’une corde puisse vibrer en plusieurs points, on aurait alors une corde avec plusieurs points de vibrations. Chaque point aurait sa propre amplitude, et ainsi les amplitudes formeraient des distinctions tout le long de la corde.

Chaque vibration a une amplitude,
une position et une propagation.
Physiquement, cette corde est engagée à s’harmoniser en fonction de ses vibrations. Elle propage un lien entre chaque vibration en influençant les points de vibration, ainsi la corde et ses vibrations interagissent mutuellement. Elle a à cause de son état, une définition globale qui peut être enrichie de multiples manières.
L’attirance créée par une vibration particulière à laquelle s’ajoute par corrélation la corde entière, produit une variation unicellulaire ayant une forte tendance à l’attraction, ainsi qu’une force fidèlement opposée comme répulsive. En comparant les points de vibration avec des objets solides, on invoquerait l’idée d’une brique polyforme plus ou moins adaptée à d’autres cordes présentant d’autres points de vibration. Et, construire un ensemble de cordes agencées selon leurs vibrations, et de cet amas ressortirait des attractions plus ou moins fortes faisant leurs effets accordés aux perceptions harmoniques de chaque partie prenante.
Les cordes n’ont pas un nombre défini de vibrations, la quantité de ces dernières varie en proportion de la corde. Plus il y a de cordes, davantage le complexe de la théorie des cordes est amplifié, c’est-à-dire que la définition globale dépend de la réalité des cordes ainsi que de celui qui produit la définition (Mais aussi pour l’adaptation des lectures)…
Le monde clustérien
Définition du dictionnaire
Le cluster est un ensemble de notes voisines formant une grappe…
Dictionnaire sur l’internet
On peut comparer une corde et un cluster, car ils ont tous deux des formes similaires. Et ceci, même si la corde a un lien physique réunissant les points de vibration. Parce que, les clusters produisent un lien métaphysique qui est produit par l’assemblage des unités.

Physiquement, la partie vide du cluster est égale au cluster, mis à part que le cluster n’est pas situé sur son emplacement. Matériellement, et plus exactement apparemment, positionné ou non, le cluster ne semble pas avoir d’expression, mis à part la régularité de son omniprésence. Mais on imagine facilement qu’un groupe uni d’unités crée une affinité de partage d’informations, ce qui ressemble à de l’éducation venant s’ajouter aux informations propres de chaque unité.
En comparaison des membres d’une même famille, qui d’ailleurs ne sont pas forcément clustérisés comme une grappe de raisin, le lien est déjà créé et l’information qui circule peut affecter chacun des membres familiaux. C’est aussi le cas des amitiés qui se forgent avec le temps tout en laissant des traces qui caractérisent les personnes, on peut s’en apercevoir dans la manière de parler tant pas les mots que par les sujets qui ressortent des amitiés.
Les deux éléments cordes et clusters, sont utiles quand on cherche à créer des combinaisons. Pour l’exemple, le développement clustérien met en évidence plusieurs méthodes de croissance clustérienne. Ne demandez pas pourquoi un développement sans intérêt puisque la réponse est claire pour le chercheur :
Tout ce qui est créé, donne une information, ce qui se révèle exact lorsqu’on a la possibilité de former un groupement en pleine croissance. Et, qui parle de croissance comprend qu’il s’agit d’une activité homogène à laquelle une limite s’impose pour ne pas fuir infiniment.
Le système tétracordique
Définition du dictionnaire :
Dictionnaire sur l’internet
L’ancienne gamme des Grecs
Comme les cordes et les clusters, les tétracordes ont une particularité qui n’a pas encore été décrite. Les tétras ont un lien logique équivalant aux cordes, ce qui fait la différence se situe dans la limitation du champ de leurs développements.
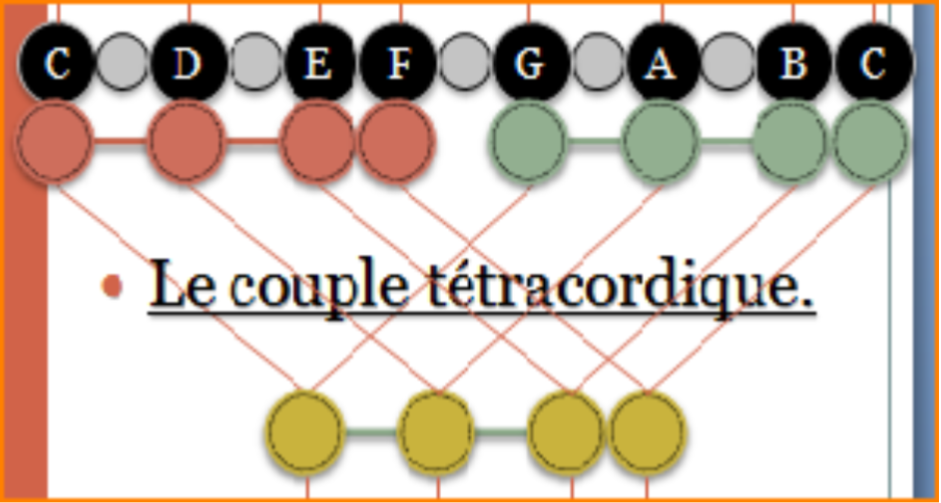
La musique est fortement détaillée
La faculté de description de la théorie de la musique est magnifique, elle attribue aux méthodes de développement de nombreuses façons de concevoir les gammes qui, en somme, constituent un grand système gammologique. Il y a des valeurs tétras, elles correspondent aux notes, qu’elles soient naturelles ou bien altérées, et ces valeurs sont couplées dans une octave. Chaque unité est conforme à la gamme heptatonique aux notes (CDEFGAB), en considérant un apport chromatique, il en résulterait deux autres éléments contenant les cinq intervalles contenus dans le couplage tétra. Ces deux pentacordes sont égaux dans l’absolu d’unités neutres, mais théoriquement parlant, ils ne sont pas identiques. Ainsi, deux tétras de 4 notes chacun, plus un penta neutre de cinq notes, somment un total de treize notes équivalant à douze demi-tons chromatiques auxquels on ajoute la note d’octave.(4 + 4 + 5 = 13)
Le tétra a également été créé à l’aide d’un algorithme Python, à cette adresse internet :
construcTetra.py (cabviva.com)
Ce code reproduit une méthode de développement appliquée sur le premier couple tétracordique, qui s’occupe de déplacer le dernier élément en premier et en pas à pas, jusqu’à ce qu’il parvienne à l’octave. Puis, l’avant-dernier niveau est avancé d’un cran, pour reproduire la même évolution au dernier élément. Cette technique de développement a été appliquée aux clusters, pendant sa période de formation à la finalisation, celle qui bâti un ensemble cohérent tout le long de son élaboration.

Exemple d’évolution routinière faisant la démonstration des chronologies respectives
Le programme construcTetra.py.pdf
Calcule les tétras un par un, selon le principe vu ci-dessus. Il y a finalement cinquante-six unités tétras produites, ce qui est suffisant pour compléter les soixante-six gammes diatoniques (y compris, les quatre-cent-soixante-deux modes). Ce résultat implique des unités tétras qui sont valables aussi bien en partie haute, qu’en partie basse, en termes de couplages tétracordiques. Le programme élabore les modèles modaux heptatoniques appliqués aux gammes, ainsi l’algorithme produit une liste de quatre-cent-soixante-deux modes. Les modes sont exprimés au format énuméré des degrés non signés, et aux emplacements non-naturels. Par un simple exemple, la gamme naturelle = 1020340506078.
--------------------------------------Champ : [['1', '2', '3', '4'], ['1', '2', '3', '0', '4'], ['1', '2', '3', '0', '0', '4'], ['1', '2', '3', '0', '0', '0', '4'], ['1', '2', '3', '0', '0', '0', '0', '4'], ['1', '2', '3', '0', '0', '0', '0', '0', '4'], ['1', '2', '0', '3', '4'], ['1', '2', '0', '3', '0', '4'], ['1', '2', '0', '3', '0', '0', '4'], ['1', '2', '0', '3', '0', '0', '0', '4'], ['1', '2', '0', '3', '0', '0', '0', '0', '4'], ['1', '2', '0', '0', '3', '4'], ['1', '2', '0', '0', '3', '0', '4'], ['1', '2', '0', '0', '3', '0', '0', '4'], ['1', '2', '0', '0', '3', '0', '0', '0', '4'], ['1', '2', '0', '0', '0', '3', '4'], ['1', '2', '0', '0', '0', '3', '0', '4'], ['1', '2', '0', '0', '0', '3', '0', '0', '4'], ['1', '2', '0', '0', '0', '0', '3', '4'], ['1', '2', '0', '0', '0', '0', '3', '0', '4'], ['1', '2', '0', '0', '0', '0', '0', '3', '4'], ['1', '0', '2', '3', '4'], ['1', '0', '2', '3', '0', '4'], ['1', '0', '2', '3', '0', '0', '4'], ['1', '0', '2', '3', '0', '0', '0', '4'], ['1', '0', '2', '3', '0', '0', '0', '0', '4'], ['1', '0', '2', '0', '3', '4'], ['1', '0', '2', '0', '3', '0', '4'], ['1', '0', '2', '0', '3', '0', '0', '4'], ['1', '0', '2', '0', '3', '0', '0', '0', '4'], ['1', '0', '2', '0', '0', '3', '4'], ['1', '0', '2', '0', '0', '3', '0', '4'], ['1', '0', '2', '0', '0', '3', '0', '0', '4'], ['1', '0', '2', '0', '0', '0', '3', '4'], ['1', '0', '2', '0', '0', '0', '3', '0', '4'], ['1', '0', '2', '0', '0', '0', '0', '3', '4'], ['1', '0', '0', '2', '3', '4'], ['1', '0', '0', '2', '3', '0', '4'], ['1', '0', '0', '2', '3', '0', '0', '4'], ['1', '0', '0', '2', '3', '0', '0', '0', '4'], ['1', '0', '0', '2', '0', '3', '4'], ['1', '0', '0', '2', '0', '3', '0', '4'], ['1', '0', '0', '2', '0', '3', '0', '0', '4'], ['1', '0', '0', '2', '0', '0', '3', '4'], ['1', '0', '0', '2', '0', '0', '3', '0', '4'], ['1', '0', '0', '2', '0', '0', '0', '3', '4'], ['1', '0', '0', '0', '2', '3', '4'], ['1', '0', '0', '0', '2', '3', '0', '4'], ['1', '0', '0', '0', '2', '3', '0', '0', '4'], ['1', '0', '0', '0', '2', '0', '3', '4'], ['1', '0', '0', '0', '2', '0', '3', '0', '4'], ['1', '0', '0', '0', '2', '0', '0', '3', '4'], ['1', '0', '0', '0', '0', '2', '3', '4'], ['1', '0', '0', '0', '0', '2', '3', '0', '4'], ['1', '0', '0', '0', '0', '2', '0', '3', '4'], ['1', '0', '0', '0', '0', '0', '2', '3', '4']]:Nombre de tétras = 56Le relevé diatonique du tétracorde
La liste précédente contient cinquante-six tétras, ils ont été développés d’une façon basiquement brute, sans distinguer les éléments provenant d’une même série diatonique.
Diatonique, stricte définition :
Vient des mots « dia » et « tonique », voulant dire ;
Dia = Signifie en divisant ou en traversant.
Dictionnaire sur l’internet
Tonique = Signifie un élément de tonalité.
En contradiction avec la définition donnée par la théorie de la musique, qui considère que la gamme chromatique est « non diatonique ». Car, la stricte définition qui est aussi démunie d’artifice supplémentaire, désigne un passage de tonalité sans en préciser un nombre, ni de valeur d’intervalle. Il est plus intelligent de ne pas détourner le sens original du mot diatonique, en lui rajoutant des significations autres que celles mentionnées dans sa qualification.
Le tétracorde a quatre éléments dont chacun d’entre eux, peut devenir un degré tonique par l’intervention d’un renversement. Comme la figure 5 le précise :
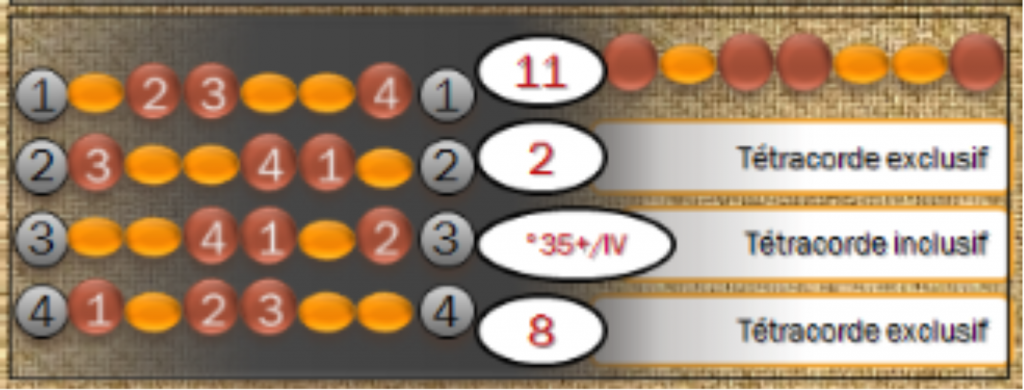
Chaque tonalité change de degré en fonction de la réponse tonique du premier degré modal relatif au tétracorde (b3 #4).
Dans l’ordre classique des degrés diatoniques au tétra mélodique amédian (#4), nous avons respectivement quatre définitions de tonalités modales pour ces notes : C, D, bE, #F.
- C -34+. DO mélodique amédian
- D -2. RÉ tonal
- bE +24. Bémol MI atonal amédian
- #F -24. Dièse FA tonal médian
Cabine harmony (cabviva.fr) : Liste les noms des gammes, selon les degrés typés.
En effet, la tonalité tétracordique change selon que le tétra est placé en partie inférieure ou supérieure, sans pour autant changer sa forme originale. Dans le développement du système tétracordique, on supervise uniquement la forme de l’objet tétra. Du fait de situer le développement dans une octave, ainsi que tout en sachant que la forme équivaut à une valeur de tonalité, elle enchaine une dépendance certaine avec les tonalités diatoniques des gammes heptatoniques. Évidemment, plutôt que de se pourvoir d’une écriture inutile, alors autant prendre son temps pour découvrir les formes tétras relatives aux gammes.
Le code Python construcTetra.py a en un premier temps établi les tétras inférieurs, qui au total groupe cinquante-six unités. Ces unités servent de base afin de produire des couples adaptés à l’intervalle d’une octave, c’est cette raison qui est invoquée lors de l’écriture des termes des recherches. Puisque au final, ne seront produites que cinquante-six gammes de couplage. La liste des cinquante-six tétras inférieurs de ci-dessus, à l’aide du code de production, déclare plusieurs types de couplages :
- “Tétra [‘C’, ‘D-2’, ‘E°3’, ‘F°4’]:[‘Gx5’, ‘A+6’, ‘B’, ‘C’] Tétra | Dia[‘1’, ‘2’, ‘3’, ‘4’] 1”
Chaque tétra se transpose en un degré analogique dont les toniques débutent toutes par la note DO, ces couples sont conçus avec des altérations. 56 unités. - “[‘1’, ‘2’, ‘3’, ‘4’, ‘0’, ‘0’, ‘0’, ‘0’, ‘0’, ‘5’, ‘6’, ‘7’, ‘8’] 1”
Construire les couplages sur les quatre-cent-soixante-deux modes, commence par se mesurer dans une formule numéraire des degrés (de 1 à 8). Ainsi, la gamme de DO majeure = [‘1’, ‘0’, ‘2’, ‘0’, ‘3’, ‘4’, ‘0’, ‘5’, ‘0’, ‘6’, ‘0’, ‘7’, ‘8’]. 462 unités. - “[‘C’, ‘D-2’, ‘E°3’, ‘F°4’, ‘Gx5’, ‘A+6’, ‘B’, ‘C’] 1”
La formule numéraire facilite l’algorithme de mutation analogique, où chaque degré numérique devient un degré analogue aux notes signées ou pas, formant une gamme en DO sortie de son champ majeur. 462 unités.
Les compliances tétracordiales
La dimension des corps tétras est limitée aux deux extrêmes, la tonique qui reste sur sa position originale représente sa limite inférieure. Et, la limite supérieure s’arrête juste avant la tonique du tétra supérieur, qui est aussi appelé le cinquième degré modal (59). Les déplacements inférieur et supérieur du quatrième degré (4) ; inf[43] et sup[48].
Tétracordes indices = [‘10‘, ‘21‘, ‘32‘, ‘43‘, ‘04‘, ‘05‘, ‘06‘, ‘07‘, ‘08‘, ‘59‘, ‘610‘, ‘711‘, ‘812‘]
La limite supérieure laisse toujours une place réservée au tétra supérieur.
Expérience personnelle
La liste de degrés tétras se détaille en faisant appel aux indices, ils représentent les positions des degrés et des intervalles en commençant par zéro. Les moments d’incrémentation des degrés du tétra inférieur, ont une limite supérieure. La limite inférieure est égale à quatre à l’indice trois, cette limite conditionne le tétra à sa plus minimaliste expression. Ainsi, quelle que soit le formulé tétra, une note de la tonalité lui est apportée en faisant en sorte que le degré du tétra corresponde au degré de la gamme choisie, en choisissant la gamme de DO :
- On reconnait plus facilement ses degrés diatoniques.
- On est sûr de ne pas se tromper dans la création.
- On évite les complications dues aux transpositions.
Il y a des conformités tétracordiques, qui ne changent que lorsqu’elles n’exercent pas la même méthode de développement. Généralement, on met en cause le sujet et sa valeur, puis pour son développement, il lui faut un espace sur lequel il peut évoluer. Le tétra a une valeur précisée par ses quatre unités, les unités quand elles ont toutes la même valeur, elles voient leurs expressions via leurs positionnements. Le sens de l’écriture est important, puisque dans les évolutions chroniques du tétracorde, il y aura toujours un premier emplacement pour déterminer un ordre itératif dans son avancement.
Le cas clustérien et son rapport de symétrisation
En développant les clusters, on rencontre des sens d’évolutions de l’écriture. En commençant par l’en haut à gauche, on avance vers la droite en bas. Ça a commencé aussi en haut et à droite, pour finir à gauche et en bas.
Avec le cluster, on a aussi commencé au milieu à partir d’en haut, pour évoluer vers une gauche et une droite symétrique. En se promenant au milieu, on pouvait détecter si le centre se trouvait sur une valeur d’une même tonalité ou plutôt dans sa moitié. Ce qui par l’exemple se traduit ainsi ;
- Dans une octave, il y a douze demi-tons dans lesquels il y a six tons. Le centre de ces douze demi-tons est situé à six demi-tons de l’octave, soit à l’emplacement de la note #FA. Ceci est valable quand le centre symétrique est situé entre DO et DO. Mais quand l’espace du développement se situe entre DO et SI, l’axe symétrique est situé alors dans un quart de ton. Ce qui change avec ces symétrisations, c’est que le milieu est placé sur une unité lorsqu’elle est en demi-ton. Et, contrairement en quart de ton, le milieu n’a pas de valeur unitaire, faisant le cas d’absence d’unité du tétracorde.
- L’âge clustérien en situation (cabviva.fr)
Le rapport du milieu avec les degrés.
Quand l’axe de symétrie est situé entre deux demi-tons,
les degrés les plus proches du milieu sont constants.
Lors d’un axe sur un demi-ton, une seule note
est constante, et elle ne subit aucune modification.

Le cas du développement diatonique
Le développement des tétracordes bien qu’il n’ait aucune contrainte, a été effectué pour répondre à un mystère d’adaptation aux gammes heptatoniques (CDEFGAB).
La méthode qui permet la création itérative par rapport aux gammes, s’applique chronologiquement comme pour les clusters ci-dessus, ce qui offre la réalisation d’un ordre croissant et une référence temporelle bien précise.
L’harmonie nous apprend à savoir que deux groupes peuvent agir, sans toutefois provenir d’une même origine. Ainsi, se croisent deux origines venant influencer les harmonies personnelles des groupes, formant un complexe doté de plusieurs harmonies (originales et personnelles). Il serait compliqué de nier les effets originaux et personnels, et les ignorer ferait un grand vide impersonnel.
Parmi toute cette profusion tétracordique, celle qui a été développée en ordre chronique, sans s’attacher à aucun autre ordre. Est une série importante de sujets en séquence ordonnée, tous les sujets ne sont pas accaparés par les gammes classiques. En tenant compte uniquement des gammes fondamentales, on diminue grandement le nombre de tétras utiles. Tout en sachant que les renversements diatoniques modaux ont tous une seule origine fondamentale, soit pour une gamme fondamentale, il y a sept degrés modaux. Si les tétras produisent une quantité de cinquante-six cas adaptés à l’intervalle d’une octave, les modèles fondamentaux n’utilisent que vingt-trois unités tétras, tout en prenant soin de ne pas omettre les tétras diatoniques obtenus par des renversements du modèle original.
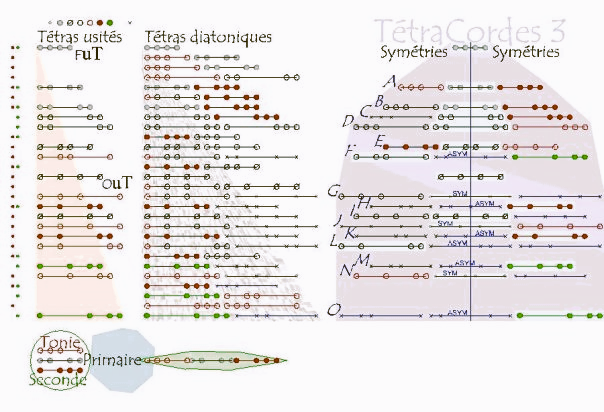
Sur la figure 7, se distingue l’ordre original croissant exercé par le programme construcTetra.py.pdf. Car, l’évolution commence par les unités de droite avant que celles de gauche entament un pas de plus. Puis, les éléments diatoniques relatifs aux tétras usités, produisent le rassemblement d’une chronologie ayant dans ses rangs des éléments situés préalablement ailleurs que leurs positions originales précédentes. Jusqu’ici, on est toujours dans un ordre primordial croissant, mais avec un classement diatonique visant à répertorier les membres d’un même tétra. Alors, la colonne des tétras diatoniques semble modifier l’ordre préétabli, en harmonisant l’expression tétra originale via une notion musicale telle la diatonie. La mise en jeu des tétras « finalisés », a gardé l’ordre des tétras usités diatonisés à l’aide d’un point de symétrisation impliquant les symétries de chacun des tétracordes.
Le cas des gammes diatoniques
Le cadre de ce sujet dépasse l’entendement des tétras diatoniques, qui par cette occasion nous expriment la vérité du terme « passer par les éléments de la tonalité ». Quand la tonalité ne concerne que les éléments, sans distinction entre leur nombre et leurs qualités.
Ce qui change avec les gammes se situe au niveau de la tonalité modale, on sait que le premier mode est appelé « tonique », parce qu’il correspond à la première note et à elle seule, puisque les autres notes suivent la constance donnée par la gamme naturelle (qui est en DO). La gamme naturelle a DO comme note en position tonique modale, et on remarquera que ce mode ne contient aucune altération, contrairement aux autres modes diatoniques. De plus et pas uniquement, si la définition modale a une signature altérative, les modalités données aux altérations prennent un essor important. Pour faire simple, les altérations modales vont de quatre dièses à cinq bémols. Aussi et classiquement, les gammes passent par les aspects « mélodiques », « dominantes », etc. Ces notions mnémoniques forment un argument de classement, pouvant définir un ordre d’évolution différent à celui donné par les signatures modales. Selon que l’un soit un type nommé de gammes, et l’autre soit une charge altérative portée. Et respectivement, le rappel des premiers éléments classiques prioritaires, le rappel de la portée altérative du premier mode naturel de la gamme.
