Définition chromatique
S’il y a une gamme qui renforce la gamme naturelle, c’est bien la gamme chromatique majeure. La gamme chromatique n’est pas naturelle puisque les notes qui la composent sont altérées, et tout le monde sait que les notes naturelles sont absolument non signées.
Il est important de ne pas dire qu’il y a qu’une seule façon de développer les gammes chromatiques, étant donné que plusieurs méthodes sont possibles. La gamme chromatique décrite par la musique classique a une définition analogique² et numérique² :
- Analogique² = Les notes de musique absolues et signées.
- Do. Ré. Mi. Fa. Sol. La. Si. Ou bien. C. #D. E. F. bbG. A. B.
- Numérique² = les formules chiffrées entières et signées.
- 1. 2. 3. 4. 5. 6. 7. Aussi bien. #2 ou +2. ##4 ou x4…
Le chromatisme a une quantification compliquée, qui ne peut exprimer avec exactitude ses compositions. Les instruments musicaux utilisés par les orchestres ne permettent pas l’expression commatique², en effet et à raison pourquoi chercher les impossibles applications sur la fréquence des notes. Alors que les instruments ne peuvent interpréter que douze notes sur plusieurs octaves, mais aussi il y a que les différences situées dans un demi-ton sont difficilement perceptibles².
- Commatique² = La gamme commatique utilise les micro-intervalles. Principalement les notes créent des enharmonies, par exemple : Do # = Ré b. L’espace de chacun des demi-tons est occupé par une note, cet écart peut être considéré comme la différence sonore perceptible par la moyenne d’écoute humaine.
- Les instruments produisent les tonalités standards basées sur douze ½ tons, ils sont aussi dotés de notes mécaniques définies par les barrettes des guitares et les touches des pianos. L’instrumentation dispose également des notes libres se jouant sur les violons (sans barrettes), les scies musicales, etc. Laissant ainsi un plus large éventail des possibilités d’interprétation, touchant ainsi les capacités auditives et des nouvelles émotions.
- L’ensemble instrumental et deux dimensions acoustiques.
- Macro-intervalle où macro est un préfixe signifiant grand.
- Micro-intervalle où micro est un préfixe signifiant petit.
- Perceptibles² = Se dit des différences perceptibles à l’écoute humaine.
COMMA : Définition de COMMA (cnrtl.fr) :- Les musiciens disent que le comma est la neuvième partie du ton
- Ils additionnent le nombre d’altérations utiles aux formes clusters extrêmes, soit : Cinq bémols pour la note 7ème et quatre dièses pour la 2ème. Ce qui fait, 5 + 4 = 9 altérations opérationnelles.
- Les musiciens disent que le comma est la neuvième partie du ton
Analogies tonales
La modulation fait l’analogie de la tonalité en accentuant la note naturelle d’une altération, démontrant une similitude partielle tout en étant fondamentalement diatonique. On peut comprendre qu’en acoustique chaque note chromatique a une définition théoriquement physique en parallèle bi ou diphasé. En rapportant ce biphasé chromatique sur une autre tessiture (macro ou micro), la similitude persistante applique des altérations aux notes originales. C’est aussi ainsi que la gamme chromatique dans sa version commatique, bien que sa similitude familière soit compréhensible, ne donnerait pas la même résolution acoustique.
Selon les modèles macro-micro venant imposer leurs propres matrices chromatiques.
Il se pourrait qu’un algorithme harmonise ces deux cas.
Mécanique macro-micro
– Macro-intervalle
La gamme tempérée – Assistance scolaire personnalisée et gratuite – ASP
'''.Gamme chromatique tempérée. Macro'''
# La valeur-unité Macro-intervalle 2**1/12 : Valeur du ½ ton
table = [55, 110, 220, 440] # Fréquences d'octaves
tonic = table[1] # Fréquence tonique 0.1=110
# Itérations de macro :
for x in range(1, 14):
note = tonic * 2**((x-1)/12)
print('x', x, 'note', note)
# Fenêtre résultat
x 1 note 110.0
x 2 note 116.54094037952248
x 3 note 123.47082531403103
x 4 note 130.8127826502993
x 5 note 138.59131548843604
x 6 note 146.8323839587038
x 7 note 155.56349186104046
x 8 note 164.81377845643496
x 9 note 174.61411571650194
x 10 note 184.9972113558172
x 11 note 195.99771799087463
x 12 note 207.65234878997256
x 13 note 220.0
– Micro-intervalle
Micro-intervalle – Encyclopédie Wikimonde
Les enharmoniques parmi les micro-intervalles (miµ)
C’est une possibilité qu’il faut envisager, l’utilité enharmonique est visible dans la gamme chromatique naturelle, lorsqu’une des notes augmentées coïncide avec une des notes diminuées. Ce cas de figure peut se répéter avec les micro-intervalles, ceci pourrait faciliter leur conception en engendrant des modulations en termes enharmoniques. Puisqu’elles existent dans un milieu où s’harmonisent un nombre considérable de gammes miµ, et alors par cela, il est préférable d’attendre que ces gammes soient développées de façon à entrevoir leurs habituelles modulations.
Je vous invite à voir les travaux que je réalise, il s’agit du développement des gammes commatiques en notes réelles. Ici on commence par les notes musicales, pour finir en un mécanisme mathématique. Les notes commatiques sont placées à l’aide de leurs qualités, seuls les intervalles réguliers sont issus d’une pure mathématique. Pages en évolution !
Premières nébuleuses commatiques aux valeurs graphiques (cabviva.fr)
– Micro-résumé
Le demi-ton a un espace réduit qui offre peu de choix aux micro-intervalles, leurs emplacements doivent (ou non) se concentrer autour de la cible laissant ainsi un moindre écart entre les cibles. Ce qui en soit cette méthode matricielle donne très peu de chance pour écouter les différences commatiques, déjà que le demi-ton a une perception de faible audition.
Ce qui fait la valeur du micro-intervalle tient dans théorie, celle qui nomme les notes précisément. Les notes commatiques ont peu de chance de se placer en domaine public selon leur écoute, elles ont toutes les chances de trouver leurs voies dans un milieu de type « micro ». Néanmoins, même si l’écoute du comma est imperceptible, à l’utilisation cette négative pourrait bien disparaitre. Puisqu’en interprétation musicale les notes sont en général éloignées les unes des autres lorsqu’elles font la mélodie, ce qui signifie que la difficulté des commas conjoints s’atténue en usage musical.
Les gammes en construction
Introduction
Il ne saurait y avoir les gammes commatiques sans les notes musicales. C’est pourquoi j’adresse un effort particulier à la conception du système commatique, qui je le rappelle est intégrée à la logique gammologique². Au vu de la quantité qualitative des gammes musicales je ne peux dire qu’elles soient évoluées, bien que les efforts de construction aient été réels lors de la période classique de la musique. Les premières théories forgent les premières mentalités, la satisfaction de ces découvertes fut grande du point de vue théorique, même si du côté public il a fallu composer des œuvres orchestrées « puisqu’il va sans dire que ces ouvrages, la reconnaissance théorique n’aurait sûrement pas connue de gloire »
- Gammologique² : Ce mot n’est pas connu des dictionnaires.
- La gammologie est la science qui effectue la découverte d’une série de sujets ou d’objets liés à un groupement, ici on parle de la gammologie des gammes musicales. Le sujet musicologique concerne l’histoire de la musique sous-forme biographique, en y plaçant un intérêt particulier pour les œuvres orchestrales, tout en éloignant la théorie de la musique par un conditionnement appliqué au solfège. Au but final de lecture des partitions musicales, je considère que la théorie de la musique est vue de façon mathématique par les fabricants d’instruments de musique.
Évolution sommaire
La gamme naturelle est un premier pas quantique², de la quantification des modulations liées aux intervalles et aux compromis diatoniques. À savoir qu’il est naturel pour la gamme de comporter sept degrés modaux, qui sont autant de modulations diatoniques. La gamme naturelle a un premier mode tonique ayant la tonalité fondamentale, contrairement aux autres modes diatoniques (à partir du second mode jusqu’au septième), qui ne supportent pas la qualité fondamentale et uniquement dans le but de discerner la tonalité gammale.
- Quantique² : La gammologie est un art de mesure quantique.
- La quantique touche la théorie de la musique (les gammes), elles sont nombreuses, précises et complexes. Les travailler est une véritable difficulté quand on sait qu’elles ont une expression libre, qu’elles font des successions d’ensembles. Jugez par vous-mêmes : La gamme naturelle engendre les 66 modes fondamentaux, qui eux-mêmes produisent 66 gammes chromatiques qui pour ensuite donner les gammes commatiques.
Vraiment, la gamme chromatique² donne une série de gammes commatiques. Le développement de la gamme chromatique peut s’effectuer de plusieurs manières, il s’agit d’un jeu trilogique (chrome augmenté, gamme originale, chrome diminué). Le chromatisme a l’avantage d’initialiser les intervalles de la gamme originale, avec précision.
- Chromatique² : Concerne l’intégralité des tonalités d’une octave.
- Par définition, la gamme chromatique relative à la gamme naturelle comporte les notes altérées situées dans les intervalles naturels, ainsi la trilogie :
| Le chromatisme augmenté | ||||||||||||
| #1 | #2 | #4 | #5 | #6 | ||||||||
| La gamme naturelle | ||||||||||||
| C | D | E | F | G | A | B | C | |||||
| Le chromatisme diminué | ||||||||||||
| b2 | b3 | b5 | b6 | b7 |
Développement chromatique
La pratique vous dira que la révolution des modes diatoniques de la gamme chromatique ci-dessus, elle vous montrera que dans son développement trilogique elle a deux choix révolutionnaires.
- La supériorité du chromatisme diminué ferme le cycle modal.
- La supériorité du chromatisme augmenté ouvre le cycle modal.
- En y apportant un modèle modal parallèle
Le chromatisme à portée des yeux (cabviva.fr)
De plus l’initialisation des intervalles non-pas par la consécutive déclarée dans le chromatisme classique, ci-dessus. Mais par la répercussion de la dernière note avant l’intervalle, par son altération progressive à chaque demi-ton. Cette méthode de développement trilogique a également deux choix révolutionnaires.
Exemple aléatoire d’un chromatisme à répercussion :
| Le chromatisme diminué | |||||||||||
| bbF | bF | bG | G | A | |||||||
| Le mode diatonique exemplaire | |||||||||||
| C | bD | bbE | F | #G | #A | B | |||||
| Le chromatisme augmenté | |||||||||||
| bE | E | #F | ##F | ##G |
La gamme chromatique majeure, complétant la gamme naturellement majeure, présente un mode chromatique tonique trilogique.
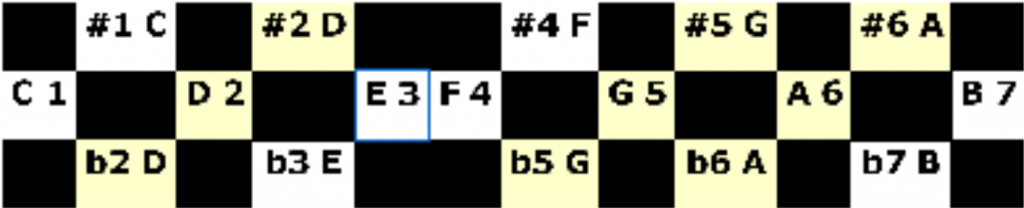
Restez vigilants, car le dièse en partie supérieure produit un modèle « ouvert »
Cabviva
Développement commatique
Elle se construit à l’aide de la gamme chromatique qui fait sa référence, parvenir à élaborer les éléments commatiques consiste à manipuler le chromatisme original.
Contenu des modes chromatiques : Notes analogiques, valeurs numériques.
En retenant uniquement les valeurs numériques, on obtient une formule qui s’adapte sur toutes les notes naturelles et altérées. Il suffit d’appliquer la note analogique à sa valeur numérique, pour la gamme naturelle qui aurait une seconde diminuée (b2) la note deviendrait (bD). Ainsi on peut ne présenter que les formules numériques modales.
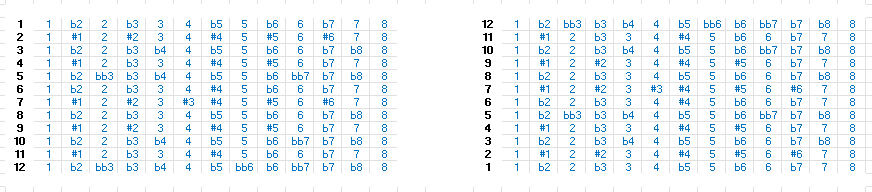
Le cycle chrome séquence bien la section de gauche, mais nous allons construire étape par étape un épisode visant l’établissement d’une matrice composite.
Composition primitive de la matrice
Étant un tableau fait de lignes et de colonnes, dont la première colonne de chaque ligne représente les notes du mode tonique chrome. Puis sur chacune des lignes on place la séquence inversée située dans la section de droite, à savoir qu’entre ces lignes on va définir les notes analogiques relatives aux formes modales numériques.
1ère colonne
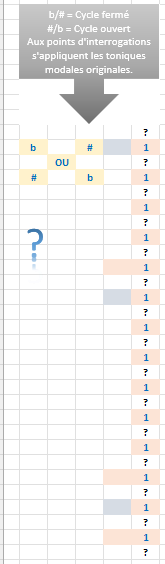
La première colonne
C’est aux points d’interrogations que viennent se mettre en situation les notes :
Soit le point d’interrogation est une note de la gamme heptatonique, celle qui fait la nature de la production et faisant un élément de traçage. Le fait de hiérarchiser nous permet de classer les innombrables définitions qui s’en suivent, d’après cette étape nous initialisons les premiers degrés sur lesquels sont portés les formes numériques.
Chaque ligne qui commence par un 1, notifie qu’à cet endroit figure la valeur de la première note de chacun des degrés modaux. Selon que le cycle soit « fermé » nous verrons que les notes analogiques des degrés voisins bien qu’elles puissent présenter quelques différences, correspondent en tous les points aux valeurs numériques de la formule.
Si vous avez l’intention de vous amuser à des variations, sachez qu’un changement s’appliquera à la production. Croyez que la rigueur du nombre infini ne tient la route qu’en étant bien structuré, alors à chaque changement pensez à la hiérarchisation. Sinon faites comme bon vous semble à vos risques et périls d’être mentalement perdu dans cette assemblée extraordinaire.
La partie constante de la matrice a maintenant tous les renseignements nécessaires au développement suivant, grâce aux données de la trilogie chromatique originale et aux lignes renseignées aux formes modales numériques inversées.
Composition initiatique de la matrice Comme dit précédemment, nous devons produire les notes analogiques de chaque degré modal, ceci autant en partie supérieure qu’inférieure
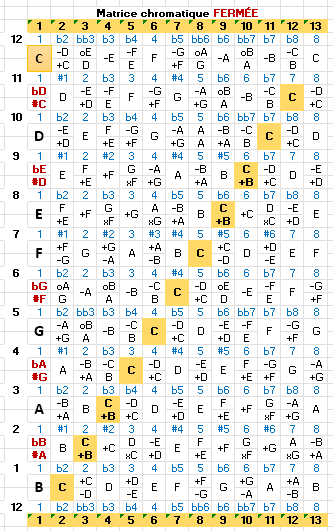
Légende de la figure 2 / La colonne des chiffres 1 à 12 = Rangs des modes numériques. Les lignes des chiffres orange 1 à 12 = Gammes commatiques
Notre première gamme commatique

La matrice complétée
Il n’y a pas longtemps, j’avais commis plusieurs erreurs parmi les notes analogiques. Elles ont été publiées et corrigées par la suite, ce qui veut dire que l’être humain peut faire des erreurs. Quand il sait il corrige, sinon oups !
Qui sont les notes sur fonds orange sur la diagonale ?
Ces notes « oranges » ont été retenues car elles se situent au même niveau que la note Do naturelle, ce qui pose un 1er pas assurément.
Ce qui ne signifie pas que ce Do soit la 1ère note tonique du degré fondamental, puisqu’à cette échelle la conception eut été mécanique. Juste en suivant les valeurs numériques.