Opération Racine carrée
Les métamorphoses des nombres
Les nombres entiers ont la particularité d’être multipliés par d’autres nombres, y compris par eux-mêmes, ce qui fait l’occasion de dire que le produit d’un même nombre donne une puissance et inversement le nombre à la puissance ½ ou 0.5 a un quotient qui représente sa racine carrée.
6 * 6 = 36 et 36 ** 0.5 = 6
Il y a sûrement plusieurs façons de calculer la racine carrée d’un nombre, qu’elles soient émises à partir d’un nombre unique ou qu’elles fassent une liste des nombres premiers.
Par exemple, si vous souhaitez connaitre les nombres communs à un seul nombre, à savoir qu’il soit le résultat produit par une pléiade de multiplications :
1 * 36 = 36
2 * 18 = 36
3 * 12 = 36
4 * 9 = 36
6 * 6 = 36
Une habitude s’est créée lors de la recherche des multiples, comme ci-dessus les opérations s’arrêtent à six qui est aussi la racine carrée de 36. Puisque ensuite les communs (6, 9, 12, 18, 36) ont déjà été calculés, et qu’ils sont considérés lors de la première phase de production. Parmi ces nombres, il y a les nombres premiers étant les premiers multiples (1, 2, 3), ces trois éléments ne rentrent pas dans le même typage de nombre premier.
Le 1 = Nombre Premier Commun Universel.
Premier (2, 3, 4, 6, 9, 12, 18, 36)
Le 2 = Nombre Premier Commun Pair.
Premier (4, 6, 12, 18, 36)
Le 3 = Nombre Premier Commun Impair & Pair.
Premier (6, 9, 12, 18, 36)
Si je considère que le chiffre un est un nombre premier, c’est parce qu’on ne peut pas le nier, il est bien un premier multiple commun universel. Il peut être multiplié et il fait partie de la grande famille des nombres, tout comme le zéro auquel on peut rattacher une fonction base dix.
La racine carrée limite
Comme on a pu le lire, la racine carrée formate le champ d’investigation du premier commun. Cette recherche œuvre dans un contexte numérique lié aux nombres en général, selon qu’on a édifié un plan de situation les réunissant. Si je vous en parle, c’est parce que ce travail a été réalisé, et qu’il renferme bien plus d’éléments de cognitifs donnés par la simple analyse d’une curiosité un peu plus poussée que d’ordinaire.
Les nombres complexes
Quand on change de technique de recherche numérale, on a le choix de diviser chaque individu numérique. Quand on choisit la division, on obtient un quotient souvent décimal, et si on rajoute à cette découverte de choisir le six comme diviseur, on voit que la partie décimale est régulière. En prenant le reste de la division par six, on a le type de nombre qui familièrement sont rangés dans cette liste (0, 1, 2, 3, 4, 5) zéro pour le six.
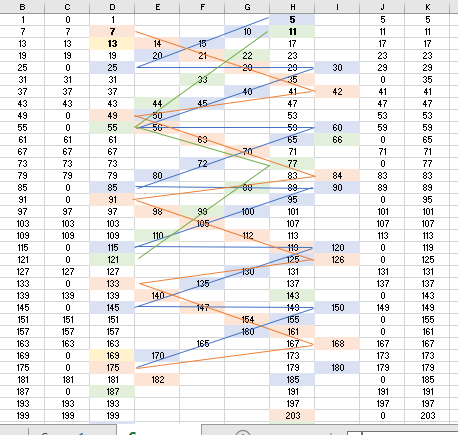
C’est ainsi que les nombres s’alignent à l’infini sur six colonnes, dont chacune des en-têtes titre les restes des divisions par six en termes numéraux.
1=1. 2=2. 3=3. 4=4. 5=5. 0=6.
Cette liste fait les liaisons des différents tempéraments des premiers multiples communs, en suivant les couleurs et les lignes aux mêmes couleurs, on suit la lecture de leurs tempéraments. Les tempéraments se croisent dans certains cas, pointant un nombre cerné par deux tempéraments différents. Si ce tableau ne précise que les nombres ayant les mêmes restes typiques à un et à cinq, c’est parce qu’il facilite la lecture des tempéraments. Autrement, sur cet affichage, on aurait pu écrire les nombres alignés sur les colonnes (2, 3, 4, 6), si ça n’a pas été fait, c’est parce que ces tempéraments n’empiètent jamais les colonnes (1, 5).
Les tempéraments numéraux
Nous venons de voir qu’il y a des tempéraments débutants sur les colonnes 1 et 5, et ceux qui commencent sur les colonnes 2 et 3 et 4 et 6. On n’a pas vu les liens qui unissent les différentes colonnes de typages, en avoir parlé et fait comprendre font deux choses opposées. Car on a dit que les tempéraments peuvent se croiser ou que des tempéraments issus de certains types n’atteignent pas certains types, pour enfin laisser planer un doute : Celui de la curiosité intellectuelle.
Les tempéraments basiques
Font partie des nombres premiers de base, ils titrent les en-têtes des colonnes (2, 3, 4, 6). Comme ils évoluent sur une ligne sur laquelle figurent six colonnes, alors sur ces lignes, nous ne pouvons trouver aucun autre premier commun, et puis une seule ligne suffit pour contenir les premiers communs qui sont 2 et 3.
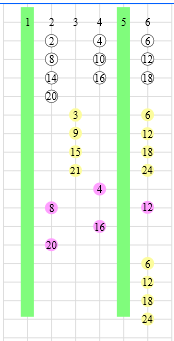
Les premiers communs élémentaires
***
Ils sont séparés pour une meilleure lecture.
On voit très nettement qu’aucun multiple n’est posé sur les colonnes 1 et 5, ce qui veut dire qu’ils ne peuvent en aucun cas mis en relation avec les nombres premiers situés sur ces colonnes ignorées.
J’ai fait une erreur jadis, en disant que les alignements verticaux ont été formés par des multiples liés aux nombres situés en haut des colonnes. Il n’y a rien à regretter puisque les mots qui décrivent la réalité peuvent changer, ainsi que vraiment les nombres du haut sont des restes de la division par six. Et qu’à chaque ligne descendue s’ajoute le chiffre six, l’exemple de la colonne quatre : (4, 10, 16, 22…)
Les tempéraments premiers
Contrairement aux tempéraments élémentaires, ils ne sont pas situés aux en-têtes des colonnes. Puisqu’ils parcourent les colonnes 1 et 5 de haut en bas. Pour résumer le parcours d’un nombre, s’il est supérieur à six son doublement sera en deuxième ligne. Si une ligne égale six ordres croissants, la quantité de lignes pour un nombre égale le nombre divisé par six. Pour le nombre 13, on aura (13 / 6) deux lignes qui sépareront chaque multiple. Ce qui pour ces cas-ci dessinent des tempéraments qui se posaient sur chacune des colonnes présentes sur le tableau.
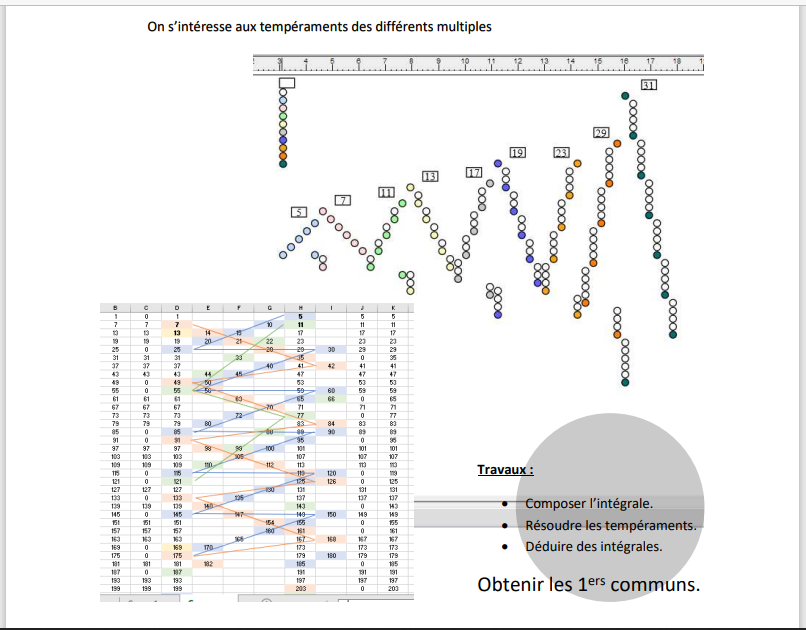
Travaux réalisés :
Il n’est pas utile de composer l’intégralité des nombres sur un tableau, cet ouvrage est pratiquement irréalisable puisque les nombres vont vers l’infini. Il suffit juste qu’il soit suffisamment renseigné, pour qu’il puisse donner les généralités définissantes les caractéristiques dégagées par les multiples.
- Un nombre premier, lorsqu’on le divise, il a un résultat décimal.
- Il faut donc chercher en amont pour lui trouver un « multiple de ».
- Comment savoir s’il n’est pas un multiple d’un autre nombre premier :
- En le divisant par sept, on saura si tel est le cas.
- En faisant le rapport de la racine carrée.
- En le divisant par cinq puis log six.
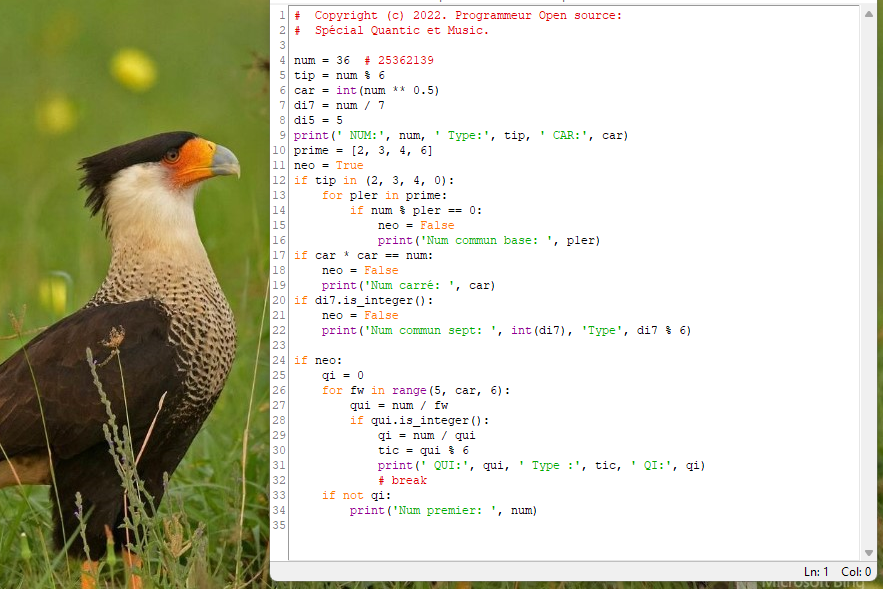
# Copyright (c) 2022. Programmeur Open source:
# Spécial Quantic et Music.
num = 2305649 # 25362139
tip = num % 6
car = int(num ** 0.5)
di7 = num / 7
di5 = 5
print(' NUM:', num, ' Type:', tip, ' CAR:', car)
prime = [2, 3, 4, 6]
neo = True
if tip in (2, 3, 4, 0):
for p1er in prime:
if num % p1er == 0:
neo = False
print('Num commun base: ', p1er)
if car * car == num:
neo = False
print('Num carré: ', car)
if di7.is_integer():
neo = False
print('Num commun sept: ', int(di7), 'Type', di7 % 6)
if neo:
qi = 0
for fw in range(5, car, 6):
qui = num / fw
if qui.is_integer():
qi = num / qui
tic = qui % 6
print(' QUI:', qui, ' Type :', tic, ' QI:', qi)
# break
if not qi:
print('Num premier: ', num)