Étant donné le travail élaboré, je suis à même de savoir le temps qu’il faudrait commencer à partir de la gamme naturelle. C’est aussi valable pour tous les mystères qu’elle a, c’est en s’adaptant à ce modèle qu’on en définit les relativités entre elles. La quantité des structures qu’elle occupe, fait que la gamme naturelle est la base d’une harmonie composée multisystémique.
Du moment où les notes de musique ont été colorisées à l’aide des couleurs de l’arc-en-ciel, ceci est un acte auquel on doit adhérer pour que la musique soit pénétrable aux couleurs du ciel. L’histoire normale dira que les premières couleurs utilisées distinguent les éléments diatoniques, et qu’elles ont changé leurs teintes naturelles.
Les mathématiques se sont rapprochées d’un algorithme à production inexpliquée, vu qu’il est simple et abordable “élémentairement parlant” comme s’il était fait pour moi.
Explication :
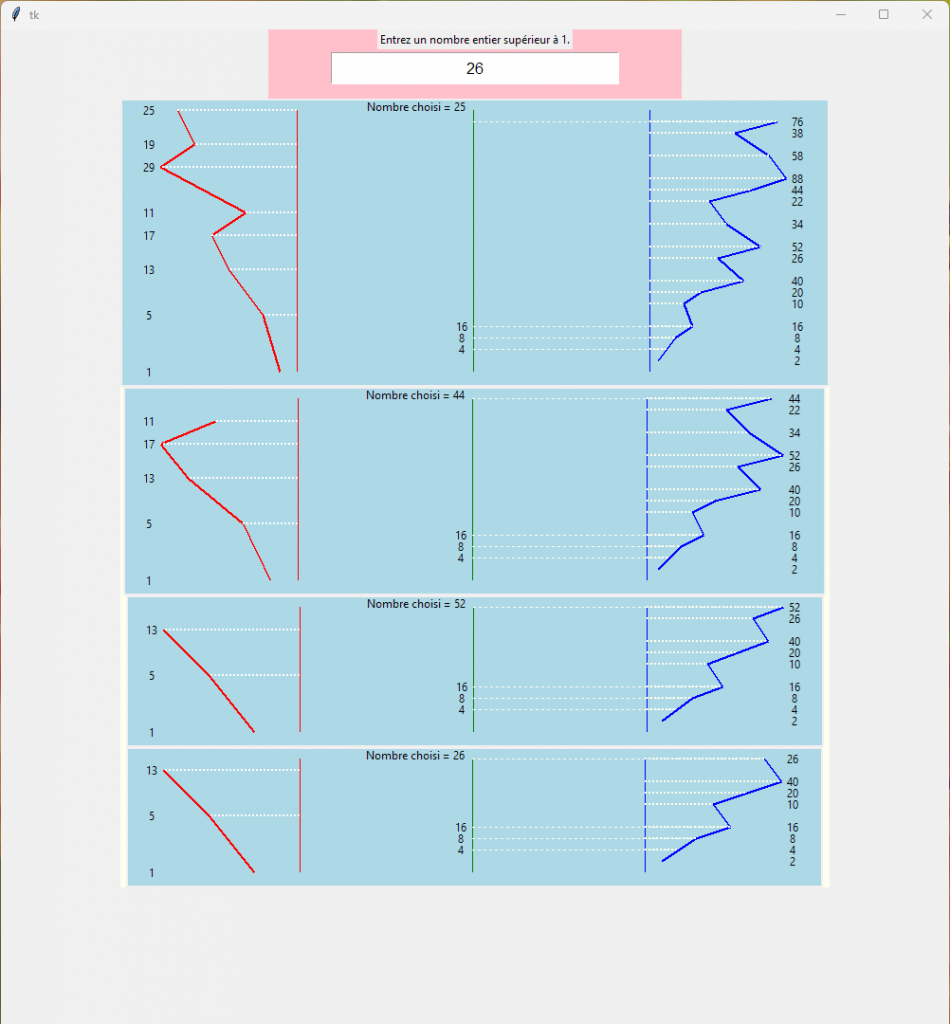
À partir d’un nombre entier compris entre 30 et 60 (pour limiter), la valeur du nombre est modifiée à chaque condition correspondante. Soit le nombre en cours est pair = Alors, il est divisé par 2, quand il est impair, le nombre impair est multiplié par trois puis on ajoute 1. Toute une série de boucles à exécuter…
'# Exemple logistique ☺'
nombre_original = 0
while 1:
# Entrée utilisateur ☺
nombre = int(input('Entrez un nombre entier supérieur à 1 : '))
nombre_original = nombre
break
'# Ici, commence (le jeu[n/2, n3+1])' quant_pairs = quant_impairs = 0 liste_pairs, liste_impairs = [], [] while nombre != 1: ('** *** *** Nombre = ', nombre)
if nombre%2 == 0:
liste_pairs.append(int(nombre))
ind = nombre
nombre = int(nombre / 2)
quant_pairs += 1
if int(nombre / 2)%2 == 0:
(ind, nombre, 'Nombre issu(n/2)après(n/2)suivant',int(nombre/2), 'pair-pair')
elif int(nombre / 2)%2 != 0:
print(ind, nombre, 'Nombre issu(n/2)après(n/2)suivant', int(nombre/2), 'pair-impair')
else:
liste_impairs.append(int(nombre))
ind = nombre
nombre = nombre * 3 + 1
quant_impairs += 1
if int(nombre / 2)%2 != 0:
print(ind, nombre,'Nombre issu(n3+1)après(n/2)suivant',int(nombre/2),'impair-impair') . elif int(nombre / 2)%2==0:
(ind,nombre,'Nombre issu(n3+1)après(n/2)suivant ', int(nombre/2), 'impair-pair')
print('Liste pairs =', liste_pairs, '\nListe impairs =', liste_impairs)
#
print("*\nNombre d'origine = ", nombre_original)
Additionner les mouvements (±) somme une différence interne.
position_cran = mouvements_pairs + mouvements_impairs
if position_cran < 0:
print("Les positifs n'ont pas rattrapés les négatifs = Négatifs gagnants ☺")
else:
print("Les positifs ont rattrapés les négatifs = Positifs gagnants ☺")
#
print('Mouvements pairs = ', mouvements_pairs, '\tmouvements_impairs = ', mouvements_impairs)
print('Et le résultat = ', position_cran)
"""Il ne reste plus qu'à expliquer pourquoi les crans descendants seront toujours en quantité supérieure."""
La logique de cette application est par rapport à un nombre, auquel un algorithme de deux traitements
‘n/2, n*3+1’. Ces deux équations conditionnées dévaluent le nombre original jusqu’à un.
À savoir que la série des nombres entiers répliquent une cadence paire et impaire, selon l’origine.
Ainsi, qu’en divisant un nombre pair par deux, on a une fois sur deux un nombre impair.
Tel qu’une fois sur deux, on descend de deux crans, soit quatre crans une fois sur deux.
Inversement, en cas d’imparité, on remonte de trois crans sans au-delà de quatre du coup (au cas-par-cas).
'''
Nombre d'origine = 9
Résultat de la liste des nombres pairs = 13
Résultat de la liste des nombres impairs = 6'''
a13 == Le nombre de fois qu’un nombre pair est traité.
b6 == Le nombre de fois qu’un nombre impair est traité.
”’
a13 = 13
b6 = 6
a13-2 § Les fois que a13 descend de deux crans. -26 b63 § Les fois que b6 monte de trois crans.
18'''”’
aa = a13-2 # Les fois que a13 descend de deux crans. bb = b63 = # Les fois que b6 monte de trois crans.
aa-bb # …
-44
bb-aa # …
44
aa # Contrôle aa
-26
bb # Contrôle bb
18
aa+bb # Négatif plus Positif
-8
bb+aa # Positif plus Négatif
-8
”’Si le résultat de aa+bb est négatif, c’est que les déplacements positifs sont inférieurs.
#