Gammologie
Quand les modulations dansent avec les notes
les nombres enrichissent le couple dansant.
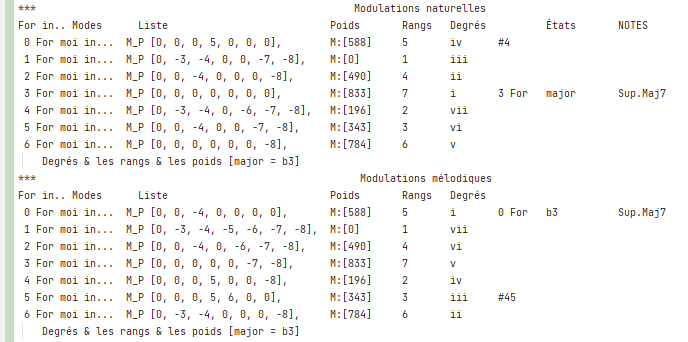
Pour moi les modulations naturelles sont devenues plus ou moins positives.
Ayant une issue diatonique, dotée du poids massif de la gamme majeure séquentielle.
« For moi in… » Modulations gamme type : Liste. Poids. Rangs. Degrés. Relevés
Ce débat musical aux résultats algorithmiques mis en forme Magviva – Magasine Cabviva folies, selon les messages contemplation 1 & 2 offrants quelques explications ou comment c’est calculé ?
Chaque mode a une masse personnelle, elle présente un poids rangé en ordre croissant. On peut aussi ranger en ordre décroissant, afin d’assembler plusieurs formes de résultat. Les degrés signalisent les emplacements toniques des gammes. La tonalité de la gamme est déterminée à éviter les signatures obscures, celles des altérations altérant les notes. Afin que sa description soit suffisamment simple et faciliter sa dénomination.
« Degrés & les rangs & les poids [major = b3] »
Ces trois orientations conversationnelles nous informent sur la nature du sujet, elles sont logiquement des conditions impliquées. Par exemple, le cas d’une série des poids correspondant à la série d’une autre diatonie.
Ooo Un moment original impliquant plusieurs paradigmes.
Des logiques paramétriques contextuellement parlantes.
Les poids et les rangs sont liés reste à prouver ?

Pour nous qui devons « comprendre » nos échanges verbaux, dans l’obligation du devoir écrit en termes de philosophie musicologique. La conservation de la musique classique prend son importance dans la formation gammologique, dont l’archivage fournit le mécanisme produit par les gammes musicologiques
« Degrés & les rangs [b25 = b24] & les poids »
Ceci est un cas où les poids ne sont pas égaux entre deux gammes, mais sauf que les rangées correspondent. Ce qui signifie, que la différence entre les poids est un parallélisme effectif. Que l’intervalle ait comme valeur une faible charge relative, ainsi que d’être mesurable au point de vue mathématique.
.B – A .A .C .B .A – B = B-A = B>A | A-B = A>B
.ʘ .406 .3 .385 .21 ! 21 où rien = ʘ
.21 .182 .2 .203 .ʘ Visuel entrelacement
.21 .672 .6 .693 .ʘ * Volet B-A. ʘ = A>B
.ʘ .651. .5 .630 .21 ( )
.ʘ .14 .1 .7 .7 1er Premier Sept
.21 .525 .4 .546 .ʘ X Trois fois Sept
.21 .966 .7 .987 .ʘ * Volet A-B. ʘ = B>A
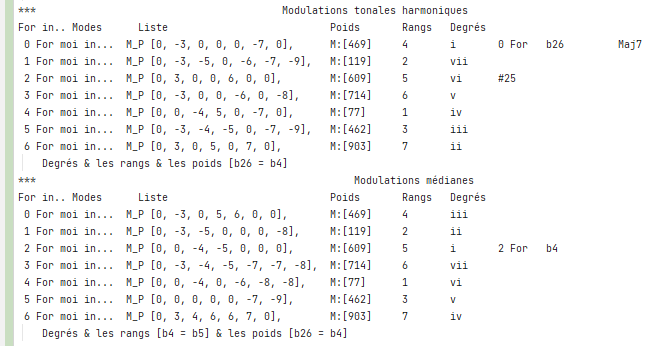
Les modulations « b26 » « b4 » ont des points identiques en mesuré du rang,
et celui du poids. Lorsque les poids sont identiques à tous les degrés,
il y a une implication sur la similitude de leurs rangements.